A kristályok alakja:
A drágakövek legnagyobb része a természetben kristályalakban található, ezért a drágakövekkel való foglalkozáshoz szükségünk van a kristálytan alapvetéseinek ismeretére. A nyers köveket sokszor már a kristályalak szempontjából, minden más segédeszköz nélkül is meghatározhatjuk.
A kristályoknak első, legszembetűnőbb sajátossága a sík lapokkal határolt alak és a lapok elrendeződésében megnyilvánuló szimmetria. A kristályok külső, szabályos felépítése és belső szerkezete között szoros összefüggés van. Ez a két tulajdonság az egyneműség, vagy homogenitás és az anizotrópia.
Homogenitás:
A homogenitás azt jelenti, hogy a kristály minden részecskéje ugyanolyan tulajdonságú, mint az egész kristály. Ha például egy kősókockát darabokra törünk, ennek minden egyes részecskéje egyforma tulajdonságú.
Anizotrópia:
A másik fontos tulajdonság az anizotrópia azt jelenti, hogy a kristályokban bizonyos tulajdonságok különböző irányokban különbözők. Így például a kristályokban bizonyos fizikai tulajdonságoknak (például keménység, összetartás a részecskék között, fénytani sajátosságok) tanulmányozásakor nem mindegy, hogy a vizsgálatokat milyen irányban végezzük, mert különböző irányokból más és más eredményeket kapunk. Az anizotrópiának különösen szembetűnő példája a kristályok hasadása. A legtöbb kristályon egy, két, vagy több olyan irány van, amelyben az összetartás, a kohézió, a kristályrészecskék közt kisebb, mint a többi irányban és a kristály a kisebb kohéziójú irányban könnyen szétválik. A kősó rendkívül jól hasad a kocka lapjainak irányában, a kalcit egy ferde kockához hasonló kristályalak, a romboéder lapjaival párhuzamos irányban.
Vannak kristályok, amelyek különböző irányokban különböző keménységűek, aminek ismerete különösen drágakőcsiszoláskor fontos. A gyémánt csiszolása is ennek a tulajdonságnak köszönhetően lehetséges, keménysége különböző irányokban más és más.
A kristályok hő hatására különböző irányokban különböző mértékben terjednek ki. Erről úgy győződhetünk meg, ha kvarcból és valamely izotróp anyagból, p. üvegből készült golyót melegítünk. Az üveggolyó minden irányban egyenletes módon terjed ki, tehát golyóalakját megtartja, míg a kvarcból készült golyó ellenben az egyik irányban megnyúlik.
Nagyon sok kristálynál tapasztaljuk, hogy különböző irányokból nézve eltérő színűek. Különösen feltűnő jelenség ez a cordieriten (iolit) és a turmalinon. A kristályok viselkedése a fénnyel szemben – jelen esetben a fény abszorbcióképésség – tehát szintén más és más a kristály különböző irányaiban.
Tipikus optikai anizotrópia figyelhet meg ezen a kiváló, 1.03 karátos, Srí Lankáról származó ioliton, AlleGem gyűjtemény. Láthatjuk, hogy bár egy szögből (szemből) nézzük a követ, mégis a szélein szürke.

Szintén különböző színeket látunk ezen a 4.91 karátos, drávit turmalinon, amely szintén Srí Lankáról származik. AlleGem gyűjtemény.

Az anizotrópiával kapcsolatos különféle jelenségek csakhamar ráterelték a figyelmet a kristályok belső szerkezetének vizsgálatára, mert nyilvánvaló volt, hogy e jelenségek okait a kristályok belső felépítésében kell keresni.
Mivel a kristályok homogén testek, legkisebb részecskéjükben is ugyanazok az anizotróp tulajdonságok nyilvánulnak meg, mint az egész kristályban, a különböző tulajdonságú irányok tehát a legkisebb részecskékben is ugyanazok, mint az egészben.
Szimmetria:
A homogenitás és az anizotrópia mellett a kristályok legszembetűnőbb tulajdonsága a kristálylapok elrendeződésében tapasztalható szimmetria. Ha egy berillkristályt figyelmesen megnézünk, azt tapasztaljuk, hogy lapjai a kristály hossztengelye körül a hatos szám szerint fejlődtek ki, még pedig a legnagyobb szabályossággal, amit a lapok által alkotott szögek mérése bizonyít. A berillkristályt hat részletben forgathatjuk a hossztengelye körül, úgy, hogy minden egyes forgatás után egyenértékű lapok ismétlődjenek. Az ilyen forgatási tengelyt hatfogásúnak nevezzük. A kristályok szimmetriája nemcsak a forgatási tengelyekre szorítkozik, hanem a kristálylapoknak tükörképileg való ismétlődésében is megnyilvánul. A kristályt egy, vagy több síkkal olyan felekre oszthatom, amelyek egymásnak tükörképei, vagyis szimmetrikusak egymáshoz.
A kristályok három fő tulajdonságára (homogenitás, anizotrópia, szimmetria) támaszkodva, tisztán elméleti úton keletkezett a kristályok belső felépítésének magyarázatára szolgáló úgynevezett térrácsteória, amely szerint a kristályt felépítő anyag elemi részei, az atomok szabályosan, egymástól bizonyos távolságra, az úgynevezett térrács alakjában a rácspontokban helyezkednek el.
Térrácsteória:
A térrácsteória beigazolását az tette lehetővé, hogy felismertük azt a hatást, amelyet a kristályok a Röntgen sugarakra gyakorolnak. A kristálylemezen áthatoló Röntgen sugarak a kristály rácsrészein elhajlásos nyalábokra bomlanak és a fényképlemezen az atomeloszlás szimmetriájának megfelelő képet idéznek elő.
Ma a legtöbb ásványnak nemcsak az atomelrendeződését, hanem az atomoknak az egymástól való távolságát is ismerjük. A térrácsok atomtávolságának a mérésére az Angström-egység szolgál, amely a centiméternek a tízmilliárdod része: 10 a mínusz tizediken cm, jele A.
Egyik legegyszerűbb térrács a kockarács, amelyben az atomok a kocka csúcspontjaiban helyezkednek el. Ismerünk ezenkívül még olyan kockarácsot is, amelyben a középpontban is van egy atom és olyan is, amelyben még minden kockalap középpontja is tartalmaz egy-egy atomot. Ez a két térrácstípus igen nagy szerepet játszik az ásványvilágban, így például a fémek legnagyobb része is ezek szerint épül fel.
A drágakövek között a gyémántnak a térrácsa két egymásba helyezett kockarács. A gyémánt nem más, mint a szén kristályosodott alakja, tehát csak egyféle atomból, szénatomokból áll, melyek a két egymásba helyezett kockarács csúcspontjaiban és lapjainak középpontjaiban helyezkednek el. Az atomok egymástól való távolsága 3,56 Angström.
A kristályok külső alakja, vagyis a kristályt határoló lapok összessége tehát tulajdonképpen a belső szerkezet kifejezője és a térrácsokban megnyilvánuló szimmetria a kristályok külső alakjában jut kifejezésre.
Kristályosztályok:
A kristályokat a rajtuk tapasztalható szimmetria alapján hét rendszerbe és ezeken belül 32 osztályba soroljuk.
Szabályos rendszer:
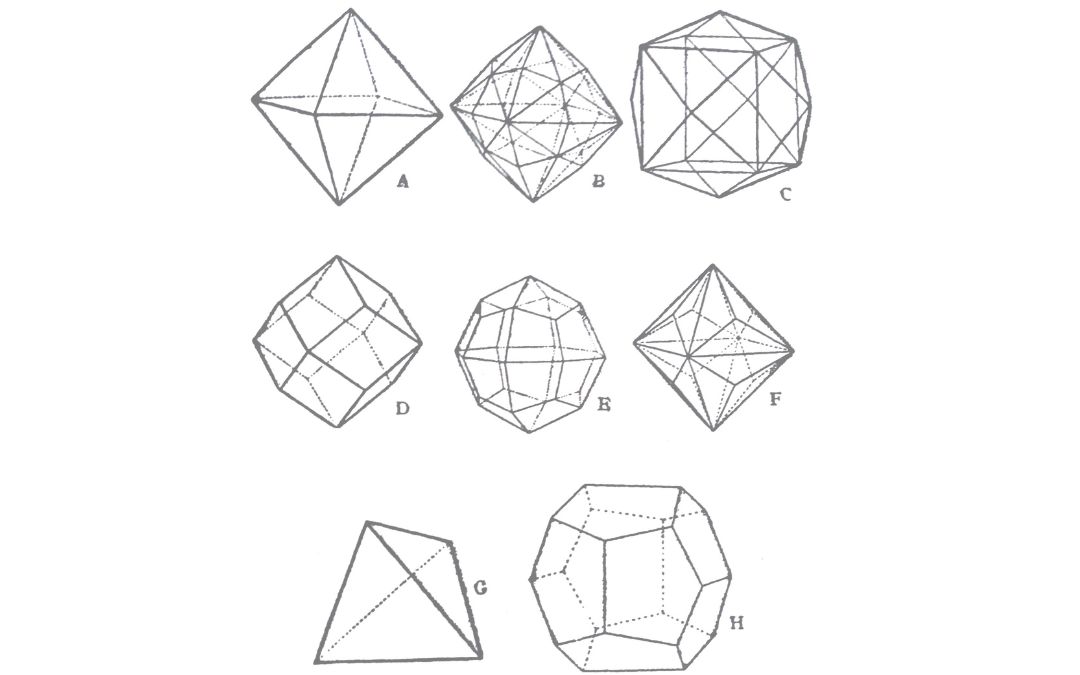
A legmagasabb szimmetriájú rendszer az úgynevezett szabályos rendszer. Vegyünk szemügyre egy kockát és képzeljük el a lapok középpontjától egy-egy egyenest a szemközt lévő lap középpontjáig. Három, egyenlő hosszú, egymást a kocka középpontjában derékszög alatt metsző tengelyt kapunk és teljesen mindegy, hogy melyik tengely áll függőlegesen és melyik vízszintesen. Mindazok a kristályok, amelyek belsejébe három ilyen tengely képzelhető, a szabályos rendszerbe tartoznak. A kocka hat lapja merőleges a tengelyekre, s mindegyik lap csak egy tengelyt metsz.
Ha a három tengely végét egy-egy lap köti össze, akkor a kristályalak nyolc egyenlő oldalú háromszögből áll és a lapok mindegyike metszi mindhárom tengelyt, mégpedig egyforma távolságban. Ez az alak az oktaéder. (A képen: „A”)
Van a szabályos rendszerben olyan alak is, amelynek a lapjai metszik ugyan mindhárom tengelyt, de mindegyiket különböző távolságban. Ebben az esetben annyi lapnak kell lennie, hogy a három különböző metszési távolság a három tengely mindkét végén meglegyen és ehhez éppen 48 lap szükséges. Ez az alak a negyvennyolcas, a hexakiszoktaéder (a képen „B”), melyen az oktaéderlap helyén hat háromszögalakú lap fejlődik ki.
Ha a lapok a két tengelyt ugyanabban a távolságban, egyet pedig ezektől különböző távolságban metszenek, akkor a lapok száma 24 lesz. Ha a két egyenlő metszési távolság a nagyobb és a harmadik a kisebb, akkor úgynevezett deltoidhuszonnégyes, vagy deltoidikozitetraéder (a képen „E”) keletkezik, amelyet 24 deltoid alakú lap alkot.
Ha pedig a két egyenlő metszési távolság a kisebb, akkor a háromszornyolchuszonnégyes, vagyis triákiszoktaéder (a képen „F”) fejlődik ki, amelyen az oktaéder egy lapjának helyén három egyenlőszárú, háromszögalakú lapot találunk.
Van azután a szabályos rendszerben még egy huszonnégylapú alak, ez a négyszerhathuszonnégyes, vagyis a tetrakiszhexaéder (a képen „C”), amelyen a hexaéder minden lapja helyén négy, egyenlő szárú, háromszögű lap fejlődik ki. Ennek az alaknak minden egyes lapja két tengelyt különböző távolságban metsz, de a harmdaikkal párhuzamos. Ha a lapok két tengelyt egyenlő távolságban metszenek és a harmadikkal párhuzamosak, akkor tizenkét lapú alak keletkezik, és ez a rombidtizenkettős, vagyis rombdodekaéder (a képen „D”), amely a gránátok jellemző alakja.
Előfordulnak még olyan alakok is, amelyek az előbb említett alakokból vezethetők le és feleannyi lapból állnak, mint az az alak, amelyből származtathatók. Ha például elképzeljük, hogy az oktaédernek csak minden második lapja fejlődik ki előttünk áll a négylapú tetraéder. (A képen „G”).
A tetrakiszhexaéderből az ötszögtizenkettős, vagyis a pentagondodekaéder vezethető le, amely a pirit közönséges alakja. (A képen „H”). Ezeket az alakokat feles alakoknak (hemiéder) nevezzük, szemben a teljes alakokkal, a holoéderekkel. Vannak negyedes alakok is, tetraoéderek is.
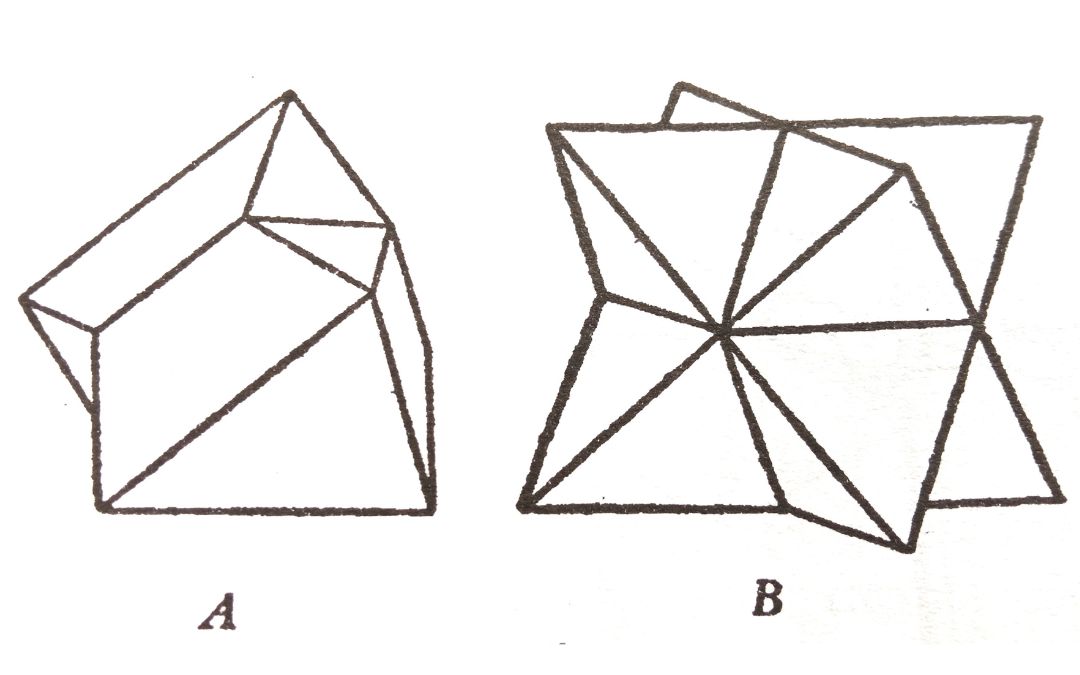
Gyakran előfordul a természetben, hogy a kristályok egymással összenőttek. Ha több kristály úgy nőtt össze, hogy az egyes kristályok kristálytani tengelyei párhuzamosak egymással, párhuzamos összenövésről beszélünk. A nem párhuzamos összenövésű kristályok közül azokat, amelyek összenövése bizonyos meghatározott törvény szerint történik, ikreknek nevezzük. Ha az ikerállásban összenőtt kristályok egyes egyéneinek helyzetét szemügyre vesszük, azt tapasztaljuk, hogy az egyik kristály helyzete a másikhoz képest egy bizonyos tengely köról 180 fokkal elforgatott. Ezt a tengelyt ikertengelynek nevezzük, az erre merőleges síkot, ikersíknak. Az ikerkristály egyik fele a másiknak a tükörképe. Az oktaédernek előfordul egy olyan ikres összenövése, amikor az egyik kristály, a másikhoz képest az egyik oktaéderlapra merőleges tengely körül 180 fokkal elforgatott helyzetben van. Ez igen gyakori a spinelleken. Ha az összenövés olyan, hogy a két kristály csak érintkezik egymással, akkor érintkezési ikerről beszélünk (a képen „A”). Ha a két kristály keresztül nő egymáson, akkor az iker átnövési, vagy penetrációs iker. A két tetraéder gyakran úgy nő egymáson keresztül, hogy az egyik kocka lapjára merőleges tengely körül a másikhoz képest 180 fokkal elforgatott (a képen „B”). Ilyen ikrekben a gyémánt fordul elő. A fluorit kockakristályai (lásd a lenti képeken) sokszor az oktaéderlap szerint nőttek egymáson keresztül.
(Sárga fluorit kristálycsoport 20*8 cm, Marokkó, AlleGem gyűjtmény.)

(Lila fluorit kristálycsoport, 15*10 cm, Marokkó, AlleGem gyűjtemény)

A drágakövek közül a szabályos rendszerben kristályosodik a gyémánt, spinell, gránát.
Négyzetes, vagy tetragonális rendszer:
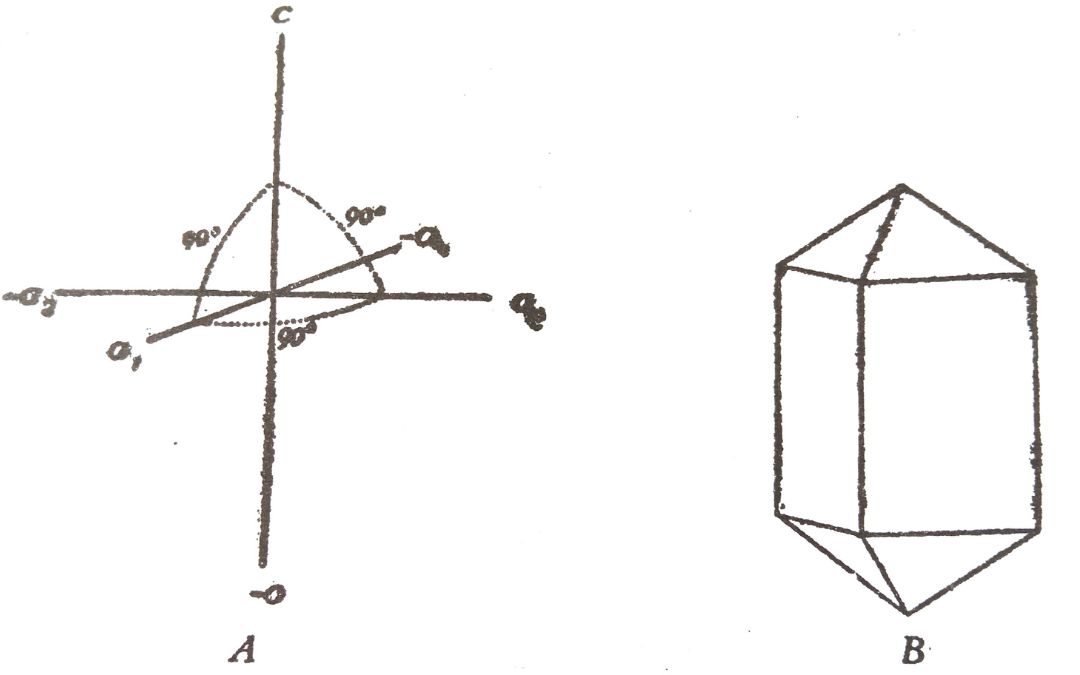
Itt szintén három egymásra merőleges tengely jellemző, amelyek közül azonban a függőleges tengely hosszabb, vagy rövidebb, mint a két vízszintes. (A képen „A”.) A vízszintes tengelyekkel párhuzamos metszetek négyzetalakúak, innen a rendszer elnevezése. Azokat az alakokat, amelyek lapjai a függőleges tengellyel – amelyet főtengelynek is nevezünk – párhuzamosak, oszlopoknak, vagy prizmáknak, a főtengelyre merőleges lappárt pedig véglapnak, vagy bázisnak nevezzük. A prizma egymagában nem alkothat kristályt, mert nyílt alak, még kevésbé a bázislapok, úgyhogy ezek csak kombinációkban jelenhetnek meg. Azok az alakok, melyeknek lapjai mind a három tengelyt metszik, a piramisok. A drágakövek közül például a cirkon és a vezúvián kristályosodik a négyzetes rendszerben (a képen „B”).
Hatszöges, vagy hexagonális rendszer:
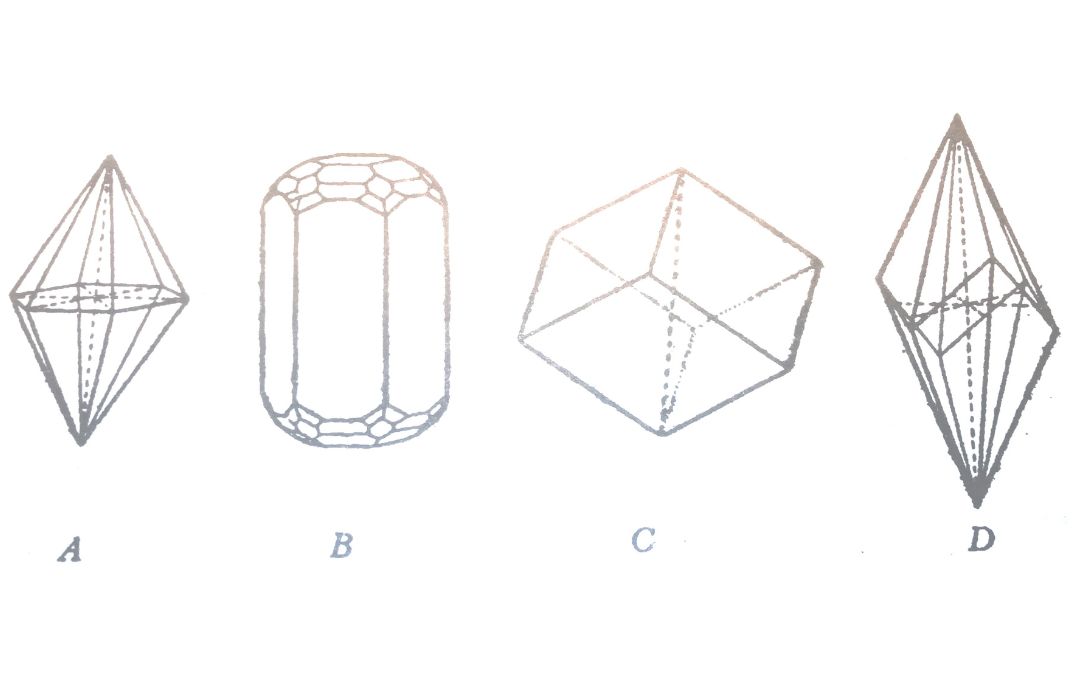
A rendszerbe tartozó kristályokba három, egymást 60 fok alatt metsző, egyforma hosszúságú vízszintes tengelyt képezhetünk s ezekre merőleges a negyedik tengely, a főtengely, amely vagy hosszabb, vagy rövidebb, mint a vízszintes tengelyek. A függőleges tengellyel párhozamos alakok itt is prizmák és e tengelyre merőleges lappárt bázisnak hívjuk. Fontosabb alakok még e rendszerben a hexagonális bipiramisok. (A képen „A”) A hatszöges rendszerben igen értékes drágakövek kristályosodnak. Ilyen a berill (a képen „B”), amelynek a rendkívül értékes változata a smaragd, továbbá a rubin, a zafír, amelyek a korund változatai.
Trigonális rendszer:
A hatszöges rendszertől el szokták különíteni azokat az alakokat, amelyeken a hármas szám uralkodik és ezeket a trigonális rendszerbe foglalják össze. Ilyen alakok a trigonális prizmák, piramisok, továbbá a romboéderek (a képen „C”), amelyeknek hat rombuszalakú lapjuk van és ferde kockához hasonlítanak, azután a szkalenoéderek (a képen „D”), amelyeket tizenkét egyenlőtlen oldalú háromszög alkot, és a trapezoéderek, amelyeket hat trapeziod alakú lap határol. A trepezoéderek a kvarc jellemző alakjai és hatoldalú oszlopokból és romboéderekből álló kombináción az oszlopnak majd a jobb, majd a bal felső sarkán jelennek meg. A trigonális rendszerbe tartoznak a turmalin és a kvarc kristályai.
Rombos rendszer:
A rombos rendszerben éppúgy, mint a szabályos, vagy a tetragonális rendszerben, három, egymásra merőleges tengely van, de ezek mindegyike különböző hosszúságú, úgyhogy egyiket sem lehet főtengelynek tartani. A teljes lapú alakok átmetszete valamelyik tengelyre merőlegesen általában rombusz. Ebben a rendszerben is vannak prizmák és piramisok, a tengelyekre merőleges lappárok a véglapok, vagy pinakoidok. A rombos rendszerben kristályosodik a topáz, valamint a krizolit, újkori nevén a peridot, vagy olivin.
Egyhajlású, vagy monoklin rendszer:
Ebben a rendszerben három különböző hosszúságú tengely közül az egyik bizonyos szög alatt hajlik. Szimmetriasík csak egy van. Ebben a rendszerben csak prizmák és véglapok vannak, amelyek mind nyílt alakok, tehát önállóan nem fordulhatnak elő, hanem csak kombinációkban. Egyhajlású ásványok az euklász, az augitok, és a földpátok egy része.
Háromhajlású, vagy triklin rendszer:
Ebben a rendszerben három különböző hosszúságú és egymást különböző szög alatt metsző tengely van. Ez a legkisebb szimmetriájú rendszer, szimmetriasík egyáltalán nincs. Az alakok csak véglapok, vagy pinakoidok, vagyis lappárok, vagy csak egyes lapok, amelyek természetesen csak kombinációkban jelenhetnek meg. Ebben a rendszerben kristályosodik a földpátok egy része, továbbá az axinit.










